I thought I’d post a few code snippets in C# that have to do with basic number theory, since I use them in my programs from time to time. These snippets are by no means optimized, and the use of C# pretty much precludes their use in high-performance applications. Still, for relatively small arguments, these routines run surprisingly fast.
Prime numbers
To generate a list of prime numbers, we use the familiar Sieve of Eratosthenes. We can write one routine to generate the sieve:
bool[] GetPrimeSieve(long upTo)
{
long sieveSize = upTo + 1;
bool[] sieve = new bool[sieveSize];
Array.Clear(sieve, 0, (int)sieveSize);
sieve[0] = true;
sieve[1] = true;
long p, max = (long)Math.Sqrt(sieveSize) + 1;
for (long i = 2; i <= max; i++)
{
if (sieve[i]) continue;
p = i + i;
while (p < sieveSize) { sieve[p] = true; p += i; }
}
return sieve;
}
The above function returns an array of booleans (the size of the given parameter), each of which is false if the array index is a prime number, or true if it's not a prime number. To get an actual list of prime numbers, we can use a function such as this:
long[] GetPrimesUpTo(long upTo)
{
if (upTo < 2) return null;
bool[] sieve = GetPrimeSieve(upTo);
long[] primes = new long[upTo + 1];
long index = 0;
for (long i = 2; i <= upTo; i++) if (!sieve[i]) primes[index++] = i;
Array.Resize(ref primes, (int)index);
return primes;
}
The above function returns an actual list of primes less than or equal to the specified high limit. This means that we can easily compute the prime-counting function $$\pi(x)$$ for any integer x by counting the number of elements in the array returned by the function. We can write a similar function to generate a list of composites:
long[] GetCompositesUpTo(long upTo)
{
if (upTo < 2) return null;
bool[] sieve = GetPrimeSieve(upTo);
long[] composites = new long[upTo + 1];
long index = 0;
for (long i = 2; i <= upTo; i++)
if (sieve[i]) composites[index++] = i;
Array.Resize(ref composites, (int)index);
return composites;
}
As for determining if a single certain number is prime (without having to generate a giant sieve), we can simply use a function that attempts to factor the number. If the number happens to be divisible by an integer greater than 1 and less than or equal to its square root, then the number is not prime:
bool IsPrime(long n)
{
long max = (long)Math.Sqrt(n);
for (long i = 2; i <= max; i++)
if (n % i == 0)
return false;
return true;
}
Greatest Common Divisor and Totient
To obtain the greatest common divisor (GCD) of two numbers, we use the usual Euclidean algorithm:
long gcd(long a, long b)
{
long temp;
while (b != 0)
{
temp = b;
b = a % b;
a = temp;
}
return a;
}
There is a slightly different binary algorithm for computing the GCD which is theoretically more efficient, but in practice (at least in C#) it's actually slightly less efficient than the algorithm above:
ulong gcdb(ulong a, ulong b)
{
int shift;
if (a == 0 || b == 0) return a | b;
for (shift = 0; ((a | b) & 1) == 0; ++shift) { a >>= 1; b >>= 1; }
while ((a & 1) == 0) a >>= 1;
do {
while ((b & 1) == 0) b >>= 1;
if (a < b) {
b -= a;
} else {
ulong temp = a - b;
a = b;
b = temp;
}
b >>= 1;
} while (b != 0);
return a << shift;
}
With the GCD readily available, determining whether two numbers are coprime is just a matter of telling whether or not their GCD is equal to 1. Also, calculating the LCM (least common multiple) of two numbers becomes trivial:
long lcm(long a, long b)
{
long ret = 0, temp = gcd(a, b);
if (temp != 0)
{
if (b > a) ret = (b / temp) * a;
else ret = (a / temp) * b;
}
return ret;
}
Also using the GCD algorithm, it becomes easy to calculate Euler's totient function for a certain number, since the totient function is simply the number of integers less than or equal to n that are coprime to n:
long eulerTotient(long n)
{
long sum = 0;
for (long i = 1; i <= n; i++)
if (gcd(i, n) == 1) sum++;
return sum;
}
The above is a really naive algorithm. A much more efficient algorithm (one that is usually given in textbooks) is as follows:
int eulerTotient(int n)
{
primes = GetPrimesUpTo(n+1); //this can be precalculated beforehand
int numPrimes = primes.Length;
int totient = n;
int currentNum = n, temp, p, prevP = 0;
for (int i = 0; i < numPrimes; i++)
{
p = (int)primes[i];
if (p > currentNum) break;
temp = currentNum / p;
if (temp * p == currentNum)
{
currentNum = temp;
i--;
if (prevP != p) { prevP = p; totient -= (totient / p); }
}
}
return totient;
}
 This book is especially significant in one other way: it contains my artwork! The book’s entry on Knight’s Tours (p. 186) familiarizes the reader with the history of this problem, dating all the way back to Euler in 1759. And, alongside the article, Pickover displays a 30×30 knight’s tour that was solved by my neural network knight’s tour implementation. For the picture in the book, I used a modified version of the program that generated a sufficiently hi-res image. That particular knight’s tour took about 3 days for my computer to generate.
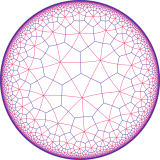
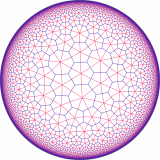
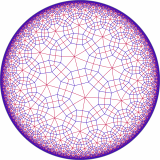
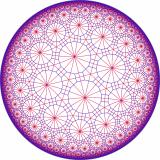
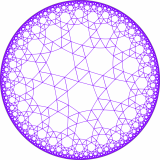
This book is especially significant in one other way: it contains my artwork! The book’s entry on Knight’s Tours (p. 186) familiarizes the reader with the history of this problem, dating all the way back to Euler in 1759. And, alongside the article, Pickover displays a 30×30 knight’s tour that was solved by my neural network knight’s tour implementation. For the picture in the book, I used a modified version of the program that generated a sufficiently hi-res image. That particular knight’s tour took about 3 days for my computer to generate.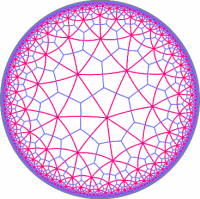 However, tessellations are also possible on non-Euclidean spaces, such as the elliptic plane (like the stitching pattern on a soccer ball), and the hyperbolic plane (like… nothing you’d find around the house). In fact, the Euclidean plane has only three regular tessellations (with squares, hexagons, and triangles), while the hyperbolic plane can be tessellated in infinitely many ways.
However, tessellations are also possible on non-Euclidean spaces, such as the elliptic plane (like the stitching pattern on a soccer ball), and the hyperbolic plane (like… nothing you’d find around the house). In fact, the Euclidean plane has only three regular tessellations (with squares, hexagons, and triangles), while the hyperbolic plane can be tessellated in infinitely many ways.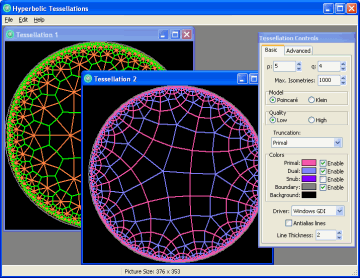
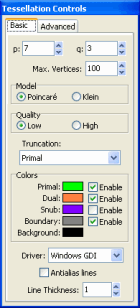 The “Tessellation Controls” window allows you to change the settings for the tessellation that is currently active.
The “Tessellation Controls” window allows you to change the settings for the tessellation that is currently active.