There was a paper in an issue of Neurocomputing that got me intrigued: it spoke of a neural network solution to the knight’s tour problem. I decided to write a quick C++ implementation to see for myself, and the results, although limited, were thoroughly fascinating.
The neural network is designed such that each legal knight’s move on the chessboard is represented by a neuron. Therefore, the network basically takes the shape of the knight’s graph over an chess board. (A knight’s graph is simply the set of all knight moves on the board)
Each neuron can be either “active” or “inactive” (output of 1 or 0). If a neuron is active, it is considered part of the solution to the knight’s tour. Once the network is started, each active neuron is configured so that it reaches a “stable” state if and only if it has exactly two neighboring neurons that are also active (otherwise, the state of the neuron changes). When the entire network is stable, a solution is obtained. The complete transition rules are as follows:
$$U_{t+1} (N_{i,j}) = U_t(N_{i,j}) + 2 – \sum_{N \in G(N_{i,j})} V_t(N)$$
$$V_{t+1} (N_{i,j}) = \left\{
\begin{array}{ll}
1 & \mbox{if}\,\, U_{t+1}(N_{i,j}) > 3\\
0 & \mbox{if}\,\, U_{t+1}(N_{i,j}) < 0\\
V_t(N_{i,j}) & \mbox{otherwise},
\end{array} \right.$$
where represents time (incrementing in discrete intervals),
is the state of the neuron connecting square
to square
,
is the output of the neuron from
to
, and
is the set of “neighbors” of the neuron (all neurons that share a vertex with
).
Initially (at ), the state of each neuron is set to 0, and the output of each neuron is set randomly to either 0 or 1. The neurons are then updated sequentially by counting squares on the chess board in row-major order and enumerating the neurons that represent knight moves out of each square.
Essentially, the network is configured to generate subgraphs of degree 2 within the knight’s graph. The set of degree-2 subgraphs naturally includes Hamiltonian circuits (re-entrant Knight’s Tours). However, there are many other solutions that would satisfy the network that are not knight’s tours. For example, the network could discover two or more small independent curcuits within the knight’s graph. In addition, there are certain cases that will cause the network to diverge (never become stable).
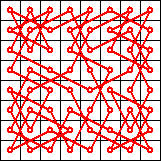

In fact, the probability of obtaining a knight’s tour on an board virtually vanishes as n grows larger. Takefuji, at the time of his publication, only obtained solutions for n < 20. Parberry was able to obtain a single knight's tour out of 40,000 trials for n = 26. I obtained one knight's tour out of about 200,000 trials for n = 28 (three days' worth of calculation on my Pentium IV). Parberry wisely asserts that attempting to find a knight's tour for n > 30 using this method would be futile.
Implementation
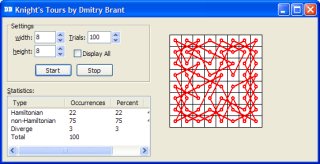
My implementation of this algorithm takes the shape of an application for Windows (although it’s perfectly runnable under Linux using wine). Several key features of the program include support for arbitrary rectangular chess boards, as well as
statistical records of trials performed.
As seen in the screenshot, the program allows you to change the width and height of the chess board. You can then adjust the number of trials to perform. Click the Start button to begin the calculation. The program will then display its progress in the statistics window on the right, showing the number of knight’s tours found, number of non-knight’s tours found, and number of divergent patterns. By default, the program draws the chess board only when a knight’s tour has been found. However, if you enable the Display All check box, the program will draw all solutions it finds.
Notable Finds
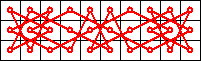 Symmetric 10 x 3 knight’s tour
Symmetric 10 x 3 knight’s tour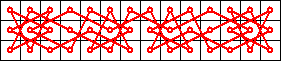 Symmetric 14 x 3 knight’s tour
Symmetric 14 x 3 knight’s tour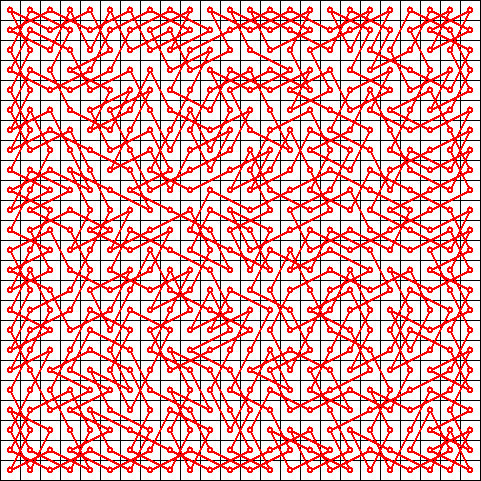 24 x 24 knight’s tour (2 hours cpu time)
24 x 24 knight’s tour (2 hours cpu time) 26 x 26 knight’s tour (8 hours cpu time)
26 x 26 knight’s tour (8 hours cpu time) 28 x 28 knight’s tour (50 hours cpu time)
28 x 28 knight’s tour (50 hours cpu time)Undoubtedly, knight’s tours for n > 28 can easily be found using simpler combinatorial algorithms, which seems to make this neural network solution for the knight’s tour problem less than practical. However, one cannot deny the inherent elegance in this kind of solution, which is what made it so interesting to investigate.
References
- I. Parberry. Scalability of a neural network for the knight’s tour problem. Neurocomputing, 12:19-34, 1996.
- Y. Takefuji and K. C. Lee. Neural network computing for knight’s tour problems. Neurocomputing, 4(5):249-254, 1992.